Free-Space¶
[1]:
import json
import pathlib
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
[2]:
!mkdir -p img
plt.rcParams.update(
{
"text.usetex": True,
"font.family": "sans-serif",
"figure.figsize": (3, 2.5),
"figure.dpi": 140,
}
)
[3]:
def load_trajectories_data(file_name=None, path=None):
path = pathlib.Path().resolve() if path is None else pathlib.Path(path)
file_name = path / file_name
assert file_name.is_file(), file_name
trajectories = json.load(open(file_name, "r"))["trajectories"]
return [np.array(trj) for trj in trajectories]
TRAJECTORIES = {
"p": load_trajectories_data("p.json"),
"q": load_trajectories_data("q.json"),
}
len(TRAJECTORIES["p"]), len(TRAJECTORIES["q"]), TRAJECTORIES["q"][0].shape
[3]:
(1024, 1, (1024, 2))
[4]:
TEST_TRAJECTORIES = {
"p": np.array([[[0, 0], [3, 4], [7, 4], [7, 8], [5, 3], [9, 3], [11, 5]]]),
"q": np.array([[[3, 0], [1, 6], [9, 6], [11, 8]]]),
}
[5]:
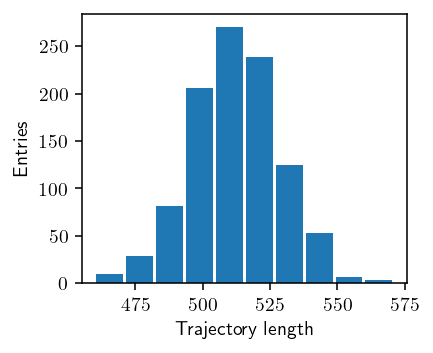
def plot_length(p):
n = [trj.shape[0] for trj in p]
fig, ax = plt.subplots()
ax.hist(n, rwidth=0.9)
ax.set_xlabel("Trajectory length")
ax.set_ylabel("Entries")
fig.savefig("img/trj_length.png")
plot_length(TRAJECTORIES["p"])
[6]:
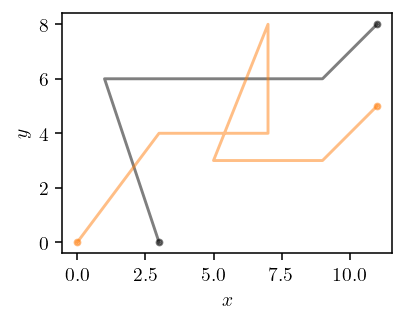
def plot_trajectories(p, q, *, p_idx, show_legend=False):
fig, ax = plt.subplots()
qx, qy = q[0].T
ax.plot(qx[0], qy[0], "k.", alpha=0.5)
ax.plot(qx[-1], qy[-1], "k.", alpha=0.5)
ax.plot(qx, qy, "k", alpha=0.5, label="$q$")
for n, i in enumerate(p_idx, start=1):
px, py = p[i].T
ax.plot(px[0], py[0], f"C{n}.", alpha=0.5)
ax.plot(px[-1], py[-1], f"C{n}.", alpha=0.5)
ax.plot(px, py, f"C{n}-", alpha=0.5, label=f"$p_{i}$")
ax.set_aspect("equal")
ax.set_xlabel("$x$")
ax.set_ylabel("$y$")
if show_legend:
ax.legend()
fig.tight_layout()
fig.savefig("img/trajectories.png")
plot_trajectories(TEST_TRAJECTORIES["p"], TEST_TRAJECTORIES["q"], p_idx=[0])
[7]:
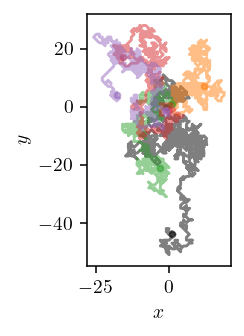
plot_trajectories(TRAJECTORIES["p"], TRAJECTORIES["q"], p_idx=[0, 1, 2, 3])
[8]:
def interpolate(points, *, n):
t = np.linspace(0, 1, n, endpoint=False)[:, np.newaxis]
return np.concatenate(
[a + (b - a) * t for a, b in zip(points[:-1], points[1:])]
+ [np.array([points[-1]])]
)
def metric(p, q):
px, py = p.T
qx, qy = q.T
return np.hypot(np.subtract.outer(px, qx), np.subtract.outer(py, qy))
[9]:
def frechet_distance(d):
P, Q = d.shape
d = np.copy(d)
d[:, 0] = np.maximum.accumulate(d[:, 0])
d[0, :] = np.maximum.accumulate(d[0, :])
path = np.zeros((P, Q, 2), dtype=np.int64)
path[1:, 0, 0] = np.arange(P - 1)
path[0, 1:, 1] = np.arange(Q - 1)
for i in range(1, P):
for j in range(1, Q):
idx = np.array([[i - 1, j], [i - 1, j - 1], [i, j - 1]])
min_idx = np.argmin(d[*idx.T])
min_idx = idx[min_idx]
d[i, j] = max(d[*min_idx], d[i, j])
path[i, j] = min_idx
optimal_path = [np.array([P - 1, Q - 1])]
while not np.all(optimal_path[-1] == np.array([0, 0])):
optimal_path.append(path[*optimal_path[-1]])
optimal_path = np.stack(optimal_path[::-1]).astype(np.float64)
return d[-1, -1], optimal_path / optimal_path[-1]
[10]:
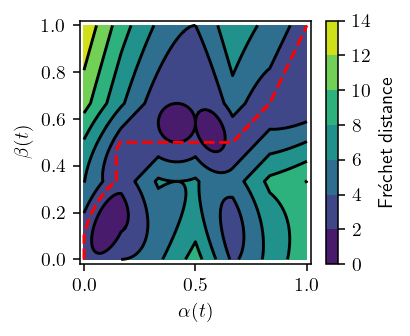
def plot_distance(p, q, *, p_idx=None, show_path=True, n=1):
if p_idx is not None:
p = p[p_idx]
p = interpolate(p, n=n)
q = interpolate(q, n=n)
d = metric(p, q)
fd, path = frechet_distance(d)
print(f"{fd=}")
tp = np.linspace(0, 1, d.shape[0])
tq = np.linspace(0, 1, d.shape[1])
x, y = np.meshgrid(tp, tq)
z = d.T
fig, ax = plt.subplots()
cset = ax.contourf(x, y, z)
ax.contour(x, y, z, cset.levels, colors="k")
cbar = fig.colorbar(cset)
if show_path:
ax.plot(path[:, 0], path[:, 1], "--", color="red")
ax.set_xlim(-0.02, 1.02)
ax.set_ylim(-0.02, 1.02)
ax.set_xlabel(
r"$\alpha(t)$" if p_idx is None else r"$\alpha_{" + str(p_idx) + "}(t)$"
)
ax.set_ylabel(r"$\beta(t)$")
cbar.set_label(r"Fr\'echet distance")
fig.tight_layout()
fig.savefig("img/distance.png")
plot_distance(TEST_TRAJECTORIES["p"][0], TEST_TRAJECTORIES["q"][0], n=100)
fd=3.000266654815868
[11]:
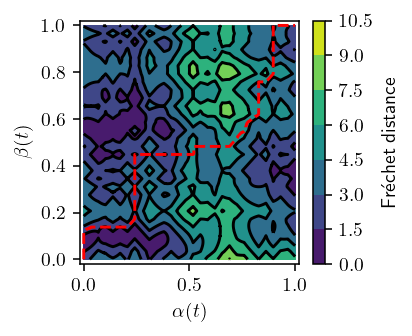
plot_distance(TRAJECTORIES["p"][0][:30], TRAJECTORIES["q"][0][:30], n=10)
fd=5.0
[12]:
def plot_freespace(p, q, *, p_idx=None, threshold=None, show_path=True, n=1):
if p_idx is not None:
p = p[p_idx]
p = interpolate(p, n=n)
q = interpolate(q, n=n)
d = metric(p, q)
fd, path = frechet_distance(d)
if threshold is None:
threshold = fd
tp = np.linspace(0, 1, d.shape[0])
tq = np.linspace(0, 1, d.shape[1])
x, y = np.meshgrid(tp, tq)
z = d.T
fig, ax = plt.subplots()
norm = mpl.colors.Normalize(vmin=np.min(z), vmax=np.max(z))
thr = norm(threshold)
sdata = [
[0.0, 1.0, 1.0],
[thr - 0.03, 1.0, 1.0],
[thr + 0.03, 0.5, 0.5],
[1.0, 0.5, 0.5],
]
my_cmap = mpl.colors.LinearSegmentedColormap(
"my_cmap",
segmentdata={"red": sdata, "green": sdata, "blue": sdata},
N=1024,
)
cset = ax.pcolormesh(x, y, z, cmap=my_cmap, norm=norm)
cbar = fig.colorbar(cset)
if show_path:
ax.plot(path[:, 0], path[:, 1], "--", color="red")
ax.set_xlim(-0.02, 1.02)
ax.set_ylim(-0.02, 1.02)
ax.set_xlabel(
r"$\alpha(t)$" if p_idx is None else "$\alpha_{" + str(p_idx) + "}(t)$"
)
ax.set_ylabel(r"$\beta(t)$")
cbar.set_label(r"Fr\'echet distance")
fig.tight_layout()
fig.savefig("img/freespace.png")
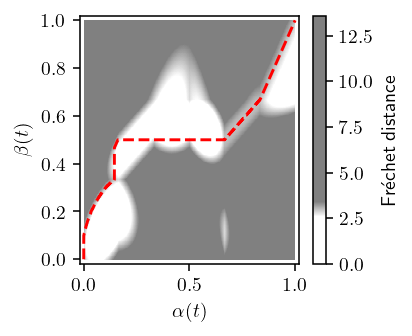
plot_freespace(TEST_TRAJECTORIES["p"][0], TEST_TRAJECTORIES["q"][0], n=100)
[13]:
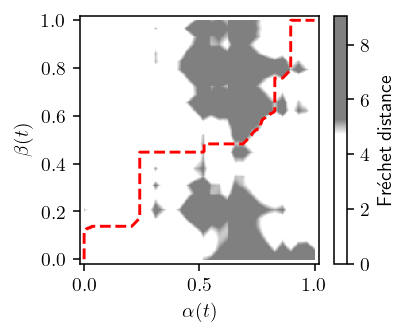
plot_freespace(TRAJECTORIES["p"][0][:30], TRAJECTORIES["q"][0][:30], n=10)
[ ]: